Keno
Keno is a famous lottery gambling game. It is played at casinos all over the world, but it is also offered by national lottery companies along with other lottery games. Explore Keno from the probability point of view.
How To Play Keno
Keno is a lottery game where there are 20 winning numbers drawn out of the total 80 numbers, while players can choose to catch 1 to 20 numbers by marking spots on a Keno ticket. It holds true that the more numbers the players attempt to catch (or hit), the higher the potential win is in case they are hit correctly.
Keno can be operated live using a traditional circular glass (aka the "bubble") or electronically (online). In case of the traditional way the bubble is filled with 80 balls and mixed by an air blower. Then 20 winning balls are drawn on random basis. At casinos Keno is played 24 hours a day in short intervals. The players are encouraged to wager by so called Keno runners.
Some casinos and lottery companies limit the choice of numbers to be hit to 10 to 15 numbers. The highest win is then paid out when a player manages to hit those 10 to 15 numbers out of the 20 drawn. Perhaps because hitting 20 numbers out of 20 is almost impossible from the probability point of view as we will see below.
Odds & Winning Chances in Keno
Thanks to the 20 numbers drawn out of 80, there is astronomic number of combinations that can be created. The easiest way to calculate all the combinations that can occur in Keno seems to use the Excel function =COMBIN(80,20) and we arrive at the value:
3,535,316,142,212,180,000.
My favorite question is: "Can you read this figure?" It is absolutely abstractionist for common calculus in common life. Alright, we can read the figure as follows:
3 quintillion 535 quadrillion 316 trillion 142 billion 212 million 180 thousand.
Just out of curiosity: If you wanted to calculate the whole number of combinations using your hand calculator and the combinatorial formula Ck(n) = n! ÷ [k! × (n – k)!], you would most likely fail. As n = 80 and k = 20, the numerator itself 80! (80 factorial) is another figure beyond understanding: 80! = 80 × 79 × 78 × ... × 1 = 7.1569×10118. That is, say, roughly seven and 118 zeros behind that! The whole formula looks like this:
C20(80) = 80! ÷ [20! × (80 – 20)!] = 7.1569×10118 ÷ (2.4329×1018 × 8.32099×1081) =.
= 3,535,316,142,212,180,000
That is as far as the total number of combinations in Keno is concerned. Then it depends on, of course, how many numbers a player attempts and manages to catch or hit. Let us pick up the most extreme case—the attempt to hit all 20 numbers out of 20.
Since there is only one winning possibility (or a combination) out of the above-mentioned total of 3.5 quintillion, the probability to hit all 20 numbers out of 20 in Keno is extremely low, almost bordering with impossibility. To be exact:
1 ÷ 3,535,316,142,212,180,000 = 0.000000000000000000282860134645.
And again, since there is only one winning combination (all the 20 numbers marked on the Keno ticket must match all the 20 drawn numbers), the total count of combination 3,535,316,142,212,180,000 is actually the fair odds (that is without margin or share of a lottery or betting company). These hypothetical odds would have to be given for the event of hitting 20 numbers out of 20. For a completion please note that the bet would have to be losing in case of fewer hits than 20 as normally you are entitled to some lower prize pursuant to a pay table.
Thus if you bet $1 and succeeded, you would win those 3.5 quintillion dollars. To get a better idea of how huge this figure is: the 2012 budget of the U.S. administration is about 2.5 trillion U.S. dollars (in revenues). It means that with the win you would be able to finance the operation of the entire U.S. for more than 1.4 million years!
Table 1 shows the probabilities and corresponding odds for a 20-spot Keno ticket.
Table 1: Probabilities and Odds for a 20-spot Keno Ticket
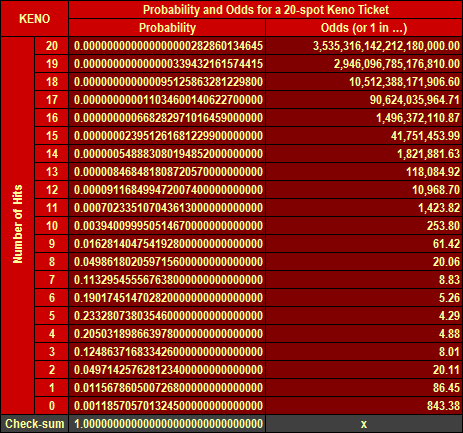
Looking at the table above, the least probable scenario is to hit all 20 numbers of out 20 – it has already been addressed in the text above. The most probable (0.2333 or 23.33% exactly) is that you manage to hit 5 numbers out of 20. Logically the most probable possibilities are usually losing. Note: the "Check-sum" means that the total of probabilities must equal one (or 100%), which is proven here.
On the other side the probability not to hit any number in Keno is roughly 0.0012 (or 0.12%) only, however this probability rises in case of fewer spot Keno tickets. Some casinos offer quite a large payouts or at least they return money if you fail to hit any number. However it varies from casino to casino, therefore it is always useful to familiarize with the pay table.
The following two tables show the probabilities and the corresponding true odds for any-spot Keno ticket, that is for all combinations of spots (1 to 20) and hits (0 to 20). Thus they are universal for any Keno game regardless of the maximum number of spots allowed. Since the tables are quite large, click to enlarge them in a new window. The calculations were done by means of MS Excel with no rounding, however only limited and relevant number of digits are displayed.
Table 2: The Probabilities for Any-spot Keno (1 to 20 Numbers)
Table 3: Odds for Any-spot Keno (1 to 20 Numbers)
Keno Pay Tables & House Edge
The choice of the amount of numbers attempting to be hit and successful hits thereof is a great source of variability as regards payouts. Additionally casinos or lottery operators may quote different payout ratios for the same wagers. Potential winnings are stipulated as multiples of the bet amount on the pay tables that have to be placed on a visible place or published online.
Various payouts present various house edges. The typical house edge ranges from 5% up to over 35%. The upper frontier is very high compared to e.g. Roulette, which brings house the share of 2.7% only. On the other hand the minimum bets are as low as $1 and potential winnings are quite high.
→ Lottery Games
→ 10 Spot Keno – Odds & House Edge
→ Powerball
→ Scratch Cards


